1. 看答案网
  2. 数学类
  3. 查看题目

下面是数学王老师布置的一到课后思考题．已知：如图1，在△ABC中，∠BAC=90°，AB=AC，点D为线段BC上一动点（不与端点B、C重合），以AD为边作正方形ADEF，连接CF．请判断CF、BC和CD的数量关

下面是数学王老师布置的一到课后思考题．已知：如图1，在△ABC中，∠BAC=90°，AB=AC，点D为线段BC上一动点（不与端点B、C重合），以AD为边作正方形ADEF，连接CF．请判断CF、BC和CD的数量关

下面是数学王老师布置的一到课后思考题．已知：如图1，在△ABC中，∠BAC=90°，AB=AC，点D为线段BC上一动点（不与端点B、C重合），以AD为边作正方形ADEF，连接CF．请判断CF、BC和CD的数量关系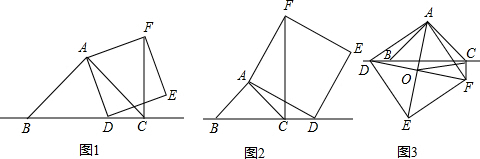．作业帮
小明思考了一会儿了，认为可以先证明△ABD≌△ACF（SAS），从而可得出CF、BC和CD的数量关系为___．（请把正确答案填在横线上）
（2）类比探究
如图2，当点D在线段BC延长线上时，其他条件不变，请判断CF、BC和CD三条线段之间的关系，并说明理由．
（3）解决问题
如图3，当D在线段BC反向延长线上时，且点A、F分别在直线BC的两侧，正方形ADEF边长为2
2
，对角线AE、DF相交于点O，并连接OC，并求OC的长．

参考答案

（1）∵∠BAC=90°，∠ABC=45°，∴∠ACB=∠ABC=45°，∴AB=AC，∵四边形ADEF是正方形，∴AD=AF，∠DAF=90°，∵∠BAD=90°-∠DAC，∠CAF=90°-∠DAC，∴∠BAD=∠CAF，则在△BAD和△CAF中，AB=AC∠BAD=∠CAFAD=AF，...

您可能感兴趣的相关题目

标签